
Resumen
En este artículo se expone como las probabilidades de existencia de un ser humano así como en general de todo nuestro Universo, son de acuerdo con los conocimientos científicos actuales, de prácticamente cero, y sin embargo es un hecho el que existamos.
Buscando un intento explicativo de lo anterior, se recurre a la teoría cuántica y a una de sus interpretaciones, la teoría del multiuniverso que, haciendo una lectura literal de dicha teoría, afirma que existen infinitos universos.
En ese mundo de infinitos universos, si sería posible la existencia de uno tan improbable como el nuestro.
Probabilidades de existencia
Es lícito preguntarse ingenuamente por la probabilidad de ocurrencia de un determinado suceso, lo que pasa es que cuando intentamos aplicar las leyes del azar a hechos tan básicos como nuestra propia existencia, aparece un profundo misterio.
Puedo preguntarme sobre mi propia existencia, y lo que diga aquí es evidentemente aplicable al lector y a cualquier otra persona. Según lo que nos dice la ciencia yo no puedo existir y sin embargo existo.
En efecto, la ciencia de la biología nos dice que para que yo exista aquí y ahora, es preciso que ocurran ciertos sucesos (o que no ocurran, por ejemplo:accidentes, enfermedades, etc…) Ahora bien hay un suceso inicial que es absolutamente necesario para que yo pueda existir y es que un determinado espermatozoide de mi padre se haya unido a un determinado óvulo de mi madre. La unión de cualesquiera otros haría surgir a un hermano mío, pero no a mí (no se consideran casos particulares como gemelos idénticos, clones, etc…)
Por otra parte la ciencia de la estadística nos permite calcular cual es la probabilidad de que se produzca la unión antes citada, dicha probabilidad se sitúa, en el cero mas favorable, en el orden de millonésimas. Es decir la probabilidad de mi concepción es pequeñísima.
Pero el problema no acaba ahí, pues para que se pueda producir dicha unión es preciso que previamente existan mi padre y mi madre, cuyas probabilidades de existencia, también en los casos mas favorables, se sitúan en el orden de millonésimas en cada caso y la probabilidad conjunta sería el producto de las tres probabilidades, es decir que para que yo pueda existir, es preciso que existan mi madre y mi padre, y que un determinado espermatozoide de uno se una a un determinado óvulo de la otra.
Pero el problema sigue, ya que para que puedan existir mis padres, es preciso que previamente existan mis abuelos y así sucesivamente, por lo que a medida que ampliamos el campo para considerar a más generaciones, la probabilidad de mi existencia tiende rápidamente a ser prácticamente cero.
Vemos pues que mi probabilidad de existencia es prácticamente nula, pero la cosa no acaba ahí, si observo una piedra en el camino y me pregunto que probabilidad de existencia tiene, la respuesta es que si consideramos todos los sucesos que han ocurrido para llegar a la existencia de esa piedra desde el Big Ban, cuando comenzó nuestro Universo, la verdad es que la probabilidad también es prácticamente cero. Podría arguirse la intervención de las Leyes de la Naturaleza, que son opuestas a los sucesos aleatorios, ya que hacen que ocurran ciertas cosas, que no se producirían por azar.
Así la interacción gravitatoria ha ejercido un papel fundamental en la existencia de esa piedra, por ejemplo: concentración gravitatoria del polvo cósmico, nacimiento de galaxias y estrellas, nuestro sistema solar, la Tierra, etc.., pero aunque sea cierto que las leyes de la Naturaleza condicionan los sucesos, la realidad nos demuestra que dentro de las condiciones de dichas leyes, se producen un enorme número de sucesos imprevistos o aleatorios, así por ejemplo la posibilidad de choques aleatorios entre asteroides que hayan producido la caída de uno de ellos a la Tierra, el cual quizá fuera el origen de la piedra si esta es meteorita, los movimientos impredecibles de las placas tectónicas de la Tierra, o de los glaciares, o de tantas cosas que hacen que la probabilidad de existencia de una piedra, pese a la acción de las leyes de la Naturaleza, siga siendo prácticamente cero.
Es decir que todo nuestro mundo, formado por infinidad de cosas y seres, es enormemente improbable que exista, y sin embargo nosotros observamos que existe.
La imposibilidad de la existencia de nuestro Universo se manifiesta también en otros aspectos como es por ejemplo el llamado "principio antrópico".
Este principio científico nos dice que el hecho de que existan los seres humanos impone restricciones a lo que es posible, no solo en nuestro entorno sino en la forma y contenido de las propias leyes de la Naturaleza.
Expongamos lo anterior de una forma distinta pero que creo es más clara; nos dice que para que existamos los seres humanos es preciso que se de una larga cadena de "felices coincidencias". Empezamos por las leyes de la Naturaleza en nuestro Universo, estas tienen que ser enormemente específicas, es decir que pequeñas variaciones en ellas nos conducirían a Universos radicalmente distintos al nuestro en los que no sería posible la vida, al menos tal como nosotros la conocemos, así por ejemplo si variase de tan solo un 0,5 por ciento la intensidad de la fuerza nuclear fuerte no existiría el carbono, pieza clave en la vida. Si la fuerza nuclear débil fuera mucho más débil de lo que es, todo el hidrógeno del Universo primitivo se habrá convertido en helio y no habría estrellas como las que conocemos. Si fuera mucho más fuerte no existirían las supernovas, tan necesarias para crear y expulsar los átomos pesados que necesitan los planetas para producir vida.
Si los protones fueran un 0,2 por 100 más pesados decaerían en neutrones y desestabilizarán los átomos. Si la suma de las masas de los tipos de quarks que constituyen un protón se modificará en tan solo un 10 por 100, la abundancia de los núcleos atómicos estables de que estamos formados sería mucho menor. De hecho la suma de las masas de esos quarks parece optimizada para la existencia del mayor número posible de núcleos estables.
Si para que pueda existir la vida, se necesita que un planeta exista al menos unos cuantos millones de años en órbitas estables alrededor de su estrella, el número de dimensiones del espacio también queda fijado por la existencia del ser humano.
En efecto, según la ley de la gravitación universal, las órbitas elípticas estables, solo son posibles en espacios de tres dimensiones, como en nuestro Universo. Las órbitas circulares son posibles con otro número de dimensiones, pero entonces resultan inestables. Para cualquier número de dimensiones espaciales excepto tres, perturbaciones pequeñas, como las que se producen por la atracción de los otros planetas del sistema solar, conduce a órbitas inestables, y producirán la expulsión de nuestro planeta de una órbita circular haciendo que caiga en espiral hacia el sol, con lo que nos abrasaríamos o bien se escapase de él también en espiral, con lo que nos helaríamos.
Por otra parte, en más de tres dimensiones la fuerza gravitatoria cae rápidamente de forma tal que el sol, no podría existir en estado estable, con su presión interna, por las reacciones termonucleares, equilibrando la compresión de la gravedad, ello significa que o bien el sol explotaría rápidamente o bien se colapsaría en un agujero negro; siendo cualquiera de las posibilidades incompatible con la vida.
Si de las leyes de la Naturaleza del Universo pasamos al Sistema Solar, también vemos que es extremadamente singular, de tal forma que no podrían existir planetas habitables como la Tierra, si el Sistema Solar fuera binario o con más soles, que es lo habitual en el Universo, pues las órbitas posibles, en un sistema de dos soles por ejemplo, son básicamente tres y ninguna de ellas permitiría un clima hospitalario, así algunas estaciones serían demasiado cálidas y otras demasiado frías para la vida.
Si las órbitas de los planetas, fueran circulares ya hemos visto que serían inestables, pero aun siendo elípticas su excentricidad debe de ser pequeña, como lo es en el caso de la Tierra que es de un solo 2 por 100, lo que junto a la inclinación del eje del planeta permite unos patrones estacionales del clima que son adecuados a la vida.
También hemos tenido suerte en relación con la masa del Sol y su distancia a la Tierra, ya que la masa de la estrella determina la cantidad de energía que libera. Las masas de las estrellas se sitúan en un intervalo de entre 100 veces más grandes o 100 veces más pequeñas que nuestro Sol y ello determinaría lo que se llama "zona habitable" de un sistema solar, es decir aquella estrecha región alrededor de la estrella en la que las temperaturas planetarias permitan la existencia de agua líquida, imprescindible para la vida. También ahí hemos sido afortunados pues la Tierra está precisamente en esa "zona habitable".
Luego el propio planeta Tierra es sumamente singular, pues posee agua líquida, imprescindible para la vida, una atmósfera rica en oxígeno y con una composición adecuada, posee un campo magnético, a diferencia de otros planetas del Sistema Solar, que protege a la vida de la radiación solar, es un planeta rocoso no gaseoso, con una gravedad y composición química también adecuada, etc.
La evolución de la vida está también llena de "felices coincidencias", empezando por la forma en que surgió la vida, que aunque desconocemos como fue, si sabemos que surgió de una forma relativamente rápida, a escala geológica se entiende.
Luego se han producido unos hechos extremadamente improbables y sorprendentes, así la vida primordial era anaerobia, es decir no utilizaba el oxígeno, pero en un momento determinado la vida produjo las algas azules o cianobacterias, que además de utilizar la energía solar para la fotosíntesis, producían oxígeno, y ello es algo realmente extraño pues el oxígeno es tóxico para la vida anaerobia y precisamente su aparición provocó probablemente la mayor catástrofe biológica que ha existido, ya que la vida primitiva casi desapareció por completo por esa causa, y surge inmediatamente la pregunta, ¿cómo pudo la vida producir algo, que al menos a corto plazo era funesto para ella?
El paso de la vida del mar a tierra firme es otro hecho sorprendente, ya que la tierra firme era estéril y no apta para la vida y tuvo que ser modificada por organismos y vegetales de origen marino para que pudiera ser habitable, especialmente por animales. Surge así otra pregunta ¿por qué la vida salió de un medio idóneo para su desarrollo, como son los mares, para colonizar y transformar un terreno estéril?
Si seguimos estudiando la evolución de la vida, vemos que las grandes extinciones masivas, de las que conocemos 5 y probablemente hubo varias decenas en toda la existencia de la vida, provocadas por caídas de meteoritos, erupciones volcánicas, cambios en la radiación solar, etc. jugaron también un papel decisivo, para que podamos existir los seres humanos sobre la Tierra, basta considerar al respecto el caso de la extinción de los dinosaurios que dio una oportunidad a los mamíferos, que probablemente no habrían tenido en caso contrario.
Para no hacer mas larga la lista no entramos en el detalle del proceso evolutivo de los seres vivos. Pero la conclusión que parece desprenderse de todo lo anterior es que nuestro Universo con la larga cadena de sucesos necesarios para la existencia de los humanos es extremadamente improbable que tenemos para ambos una probabilidad de existencia que es prácticamente cero.
Dejemos el tema ahí y pasamos a estudiar otra cuestión que quizás nos ayude a la comprensión de la realidad, sea esta la que sea.
El Multiuniverso
En los años 20 del siglo XX, diversos físicos como Plank, Heisemberg, Schroedinger, etc. desarrollaron la teoría cuántica, también llamada mecánica cuántica, para contraponerla a la física de Newton o mecánica clásica.
Esta teoría es sumamente compleja y contraintuitiva y como dice Feyman, famoso científico cuántico, "nadie entiende la mecánica cuántica", así que no voy a tener la presunción de decir que la comprendo, ni mucho menos, lo que hago a continuación es presentar, espero sin demasiados desaciertos, las opiniones de algunos autores versados sobre la materia, que me han parecido interesantes.
Actualmente la mecánica cuántica no es solo uno de los grandes pilares de la física moderna, sino que una gran parte de la economía mundial (parte que algunos autores estimen en un 25% del total) se basan en la misma.
La mecánica cuántica es una formulación matemática que parece ser científicamente cierta, en el sentido que sus predicciones coinciden con los resultados experimentales efectuados, al menos hasta ahora.
Como hemos dicho el formulismo matemático de esta teoría funciona y hay consenso entre los físicos al respecto, el problema surge si nos planteamos que es lo que nos quieren decir dichas ecuaciones sobre la realidad de nuestro mundo.
Así pues el auténtico problema es interpretar una teoría tan extraña. A este respecto han surgido múltiples interpretaciones, siendo quizás la más comúnmente aceptada la llamada de Copenhagen que viene a decir: no te preocupes de filosofías y utiliza sus cálculos. Pero claro, una visión pragmática como la anterior no satisface a muchos científicos que han tratado de desentrañar lo que realmente nos está diciendo. Como hemos indicado hay múltiples interpretaciones, quizás diez principales y muchas otras secundarias.
Entre estas interpretaciones se encuentra la llamada teoría del Multiuniverso. Esta teoría hace una lectura literal de la teoría cuántica, así autores como Hugh Everett y otros dicen que en realidad existen infinitos Universos; que todas las diferentes probabilidades de una función de ondas de un átomo, son reales cada una en un mundo diferente. Consideran que todo lo que pueda ocurrir al evolucionar una función de ondas, ocurre. Así en el celebre ejemplo del gato de Schroduger el animal está simultáneamente vivo y muerto, pero en dos mundos diferentes.
Un mundo de infinitos Universos, es compatible con la probabilidad de existencia prácticamente nula de nuestro Universo, ya que uno de los infinitos Universos podría ser el nuestro, aquel en que nosotros somos los observadores y en el que se dan todos los improbables sucesos que llevan hasta nosotros.
La mareante perspectiva que abre la anterior teoría no es la única interpretación asombrosa de la teoría cuántica, así por ejemplo nos dice también que un átomo no es real, que consiste en una función de onda de potencialidades y que solo se hace real cuando es observado.
Esta interpretación a pesar de su aparente extrañeza, es sostenida con diferentes terminologías (colapso, decoherencia, etc…) por prácticamente todos los autores cuánticos que he leído.
La observación tiene una parte principal, según Von Neuman, que es la libre elección por parte del ser humano de cómo y cuándo va a efectuar la observación. Estas libres elecciones son las que originan que un fenómeno cuántico se haga realidad, es decir son las que crean la realidad.
También nos dice que cuando una observación hace real un suceso, éste no solo consiste en una situación aquí y ahora, sino que hace real asimismo su pasado, su historia, es decir la cadena específica de sucesos, que desde el principio de los tiempos conduce al suceso actual.
Lo anterior ha llevado a algunos autores como Fred Hoyle o Martin Rees a defender el llamado principio antrópico fuerte (a diferencia del que hemos expuesto anteriormente, que es el débil), este principio dice que es el observador, el ser humano, el que causa la existencia real del Universo.
Así se produce un cambio brutal de nuestra concepción de la realidad, desde una visión intuitiva y clara que nos daba la física clásica en la que el Universo, externo a nosotros, era algo real e independiente y en el que el hombre no era su centro, como tampoco lo era la Tierra (teoría geocéntrica) o el sistema solar (teoría heliocéntrica). Se pasa así a otras posibles concepciones del universo, extrañas y difíciles de aceptar, en las que el mundo externo e interno del ser humano estaría profundamente interrelacionados.
Para terminar esta breve exposición de algunas interpretaciones de la mecánica cuántica, que sin duda producirán en el lector, como mínimo, perplejidad, no quedaría el cuadro completo si no tratáramos de incluir el concepto de Dios en él, especialmente cuando los físicos cuánticos son muchos de ellos ateos o agnósticos, por ello me ha parecido interesante incluir a este respecto unas frases de Henry Stapp, reputado físico cuántico de la universidad de California:
"…Las libres elecciones hechas por el observador humano, pueden ser vistas como versiones en miniatura, de las elecciones que parecen ser necesarias para la creación del universo. La teoría cuántica abre la puerta a, y en verdad necesita, que se hagan dichas libres elecciones.
Esta situación es concordante con la idea de un poderoso Dios que crea el Universo y sus leyes, para que todo empiece, pero después lega parte de su poder a un ser creado a su imagen…"
Bibliografía
- Chancho Neve, José Luis (2008) "Reflexiones sobre el mundo y el ser humano" Huerga y Fierro Editores.
- Chancho Neve, José Luis (2012) "Crítica estadística de la hipótesis de mutación aleatoria y espontánea como origen de la evolución". "El enigma de la vida". "La conciencia en los seres vivos". "La intervención biológica". www.monografias.com.
- Davies Paul y otros (2010) "Information and the nature of reality". Cambridge University Press.
- Hawking, Stephen (2010) "El gran diseño". Ed. Crítica.
- Penrose, Roger (2007) "El camino de la realidad". Random Houre Mondadori.
- Rosen Blum, Bruce y otro (2010) "El enigma cuántico". Turquets Editors.
- Vedral Vlatko (2011) "Descodificando la realidad". Biblioteca Burdan.
- Velarde, Guillermo (2002) "Mecánica cuántica". Mcgraw Hill.









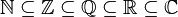
 , una versión de la letra griega
, una versión de la letra griega  (épsilon). Los segundos argumentos de la relación
(épsilon). Los segundos argumentos de la relación  se cumple, se dice que
se cumple, se dice que  es un elemento del conjunto
es un elemento del conjunto  . Si aceptamos que todo es un conjunto, entonces los primeros y segundos argumentos de
. Si aceptamos que todo es un conjunto, entonces los primeros y segundos argumentos de  .
.













