
LO IMPRESCINDIBLE:
Lo imprescindible es que algo para realizarse, para actuar, para funcionar, para su desarrollo, para que exista, NECESITA de la intervención de un actor esencial que es lo que lo inicia, lo que lo continúa, lo que lo lleva a una finalidad -a una acción concreta consecuencial a sus actos-. Sí, es un inductor de su acción.
Para un coche, así, lo imprescindible es una energía que lo induce a ser realmente coche; y antes no, solo con la energía ya es... real su acción específica de coche.
Para el MOVIMIENTO ocurre igual; claro, algo no es movimiento hasta que no hayan: ESPACIO e INTERACCIÓN. Es decir, siempre y cuando haya espacio y algún tipo de interacción, pues -solo así- hay movimiento.
Y, para eso, no hace falta señalar qué tipo de interacción, no, si de la materia oscura, si de tales partículas o si de tales cuerpos celestes; porque, para que exista movimiento, es suficiente espacio e interacción -sea cual sea-: es la base imprescindible.
Una vez ahí, la acción consecuencial de la interacción con el espacio -que va cambiando, aumentando o disminuyendo- se desarrolla de la determinada y única manera que es propia de ese espacio (espacio denso o espacio menos denso o espacio reduciéndose o aumentando con la interacción, esto es, porque siempre el espacio es... el espacio de la interacción, de cualquiera; eso es el espacio, no existe espacio no-espacio o espacio puramente vacío, sin él mismo, pues... eso sería nada pura, o sea, inexistencia y la inexistencia del mismo espacio, ¿lo comprenden?).
Cierto, la interacción está determinada -en consecuencia- a la condición propia del espacio: a tener más inercia o a tener menos inercia. Es, en claro, la condición inercial de un espacio la determinante de la siguiente interacción que haya en ese espacio.
Un punto subatómico muy denso, por ejemplo, va teniendo tan poquísima INERCIA progresivamente -o mucha interacción progresiva- que eso induce o inducirá, en ese ir comprimiendo o reduciendo o consumando o eliminado su propio espacio, a un instante en el cual, por asegurar lo imprescindible siempre de que exista espacio-interacción, ya en el punto extremo de consumado el suyo, ha de crear un nuevo espacio.
Es la inducción extrema -el hecho consecuencial- de: un continuo aumento de la interacción en una continua reducción -o eliminación o consumación- de su propio espacio. Eso es, es la CONSECUENCIA ÚLTIMA -en ese contexto- que no puede prescindir aún de lo imprescindible porque exista ese movimiento mismo; y ha de crear otro espacio, que conllevará -cierto- una nueva condicionalidad.
- Un espacio denso tiene menos inercia y más capacidad para cambiar su estado inmediatamente anterior.
- Un espacio menos denso tiene menor interacción -o menor capacidad o rapidez para cambiar-; todo sucede más lento y, por tanto, más resistencia presenta para cambiar sus estados o sus estados "en reposo". Es decir, tiene más inercia, menor movimiento.
Lo imprescindible es que algo para realizarse, para actuar, para funcionar, para su desarrollo, para que exista, NECESITA de la intervención de un actor esencial que es lo que lo inicia, lo que lo continúa, lo que lo lleva a una finalidad -a una acción concreta consecuencial a sus actos-. Sí, es un inductor de su acción.
Para un coche, así, lo imprescindible es una energía que lo induce a ser realmente coche; y antes no, solo con la energía ya es... real su acción específica de coche.
Para el MOVIMIENTO ocurre igual; claro, algo no es movimiento hasta que no hayan: ESPACIO e INTERACCIÓN. Es decir, siempre y cuando haya espacio y algún tipo de interacción, pues -solo así- hay movimiento.
Y, para eso, no hace falta señalar qué tipo de interacción, no, si de la materia oscura, si de tales partículas o si de tales cuerpos celestes; porque, para que exista movimiento, es suficiente espacio e interacción -sea cual sea-: es la base imprescindible.
Una vez ahí, la acción consecuencial de la interacción con el espacio -que va cambiando, aumentando o disminuyendo- se desarrolla de la determinada y única manera que es propia de ese espacio (espacio denso o espacio menos denso o espacio reduciéndose o aumentando con la interacción, esto es, porque siempre el espacio es... el espacio de la interacción, de cualquiera; eso es el espacio, no existe espacio no-espacio o espacio puramente vacío, sin él mismo, pues... eso sería nada pura, o sea, inexistencia y la inexistencia del mismo espacio, ¿lo comprenden?).
Cierto, la interacción está determinada -en consecuencia- a la condición propia del espacio: a tener más inercia o a tener menos inercia. Es, en claro, la condición inercial de un espacio la determinante de la siguiente interacción que haya en ese espacio.
Un punto subatómico muy denso, por ejemplo, va teniendo tan poquísima INERCIA progresivamente -o mucha interacción progresiva- que eso induce o inducirá, en ese ir comprimiendo o reduciendo o consumando o eliminado su propio espacio, a un instante en el cual, por asegurar lo imprescindible siempre de que exista espacio-interacción, ya en el punto extremo de consumado el suyo, ha de crear un nuevo espacio.
Es la inducción extrema -el hecho consecuencial- de: un continuo aumento de la interacción en una continua reducción -o eliminación o consumación- de su propio espacio. Eso es, es la CONSECUENCIA ÚLTIMA -en ese contexto- que no puede prescindir aún de lo imprescindible porque exista ese movimiento mismo; y ha de crear otro espacio, que conllevará -cierto- una nueva condicionalidad.
- Un espacio denso tiene menos inercia y más capacidad para cambiar su estado inmediatamente anterior.
- Un espacio menos denso tiene menor interacción -o menor capacidad o rapidez para cambiar-; todo sucede más lento y, por tanto, más resistencia presenta para cambiar sus estados o sus estados "en reposo". Es decir, tiene más inercia, menor movimiento.
28 DE OCTUBRE DE 2012
PUBLICADO POR JOSÉ REPISO
http://ensayosobreteoriarelatividad.blogspot.com.es/2012/10/lo-imprescindible-lo-imprescindible-es.html
---
**Visita: http://bohemiaylibre.blogspot.com




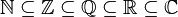
 , una versión de la letra griega
, una versión de la letra griega  (épsilon). Los segundos argumentos de la relación
(épsilon). Los segundos argumentos de la relación  se cumple, se dice que
se cumple, se dice que  es un elemento del conjunto
es un elemento del conjunto  . Si aceptamos que todo es un conjunto, entonces los primeros y segundos argumentos de
. Si aceptamos que todo es un conjunto, entonces los primeros y segundos argumentos de  .
.








